散列(hash)

在一个域(一个集合)中，其中存在着一个实际域，包含着我们所实际用到的元素，如自然数是一个域，其中我们有一个实际域，比如说{1,2,3}。这些作为关键字指向元素，这里的关键字就是指数组的下标一样的东西，根据一个关键字，我们就可以得到它所指的元素。

当全域较小的时候，我们可以之间建立一个表，一一对应。

但是当全域较大但是实际域并不大的时候，这就过于浪费存储空间了，因为很多的关键字都对应着NIL(空)，因此，我们可以通过一个散列表来建立关系。

散列表是通过一个散列函数$h(x)$来建立对应关系的。

但是不管怎么样，只要我们散列表所

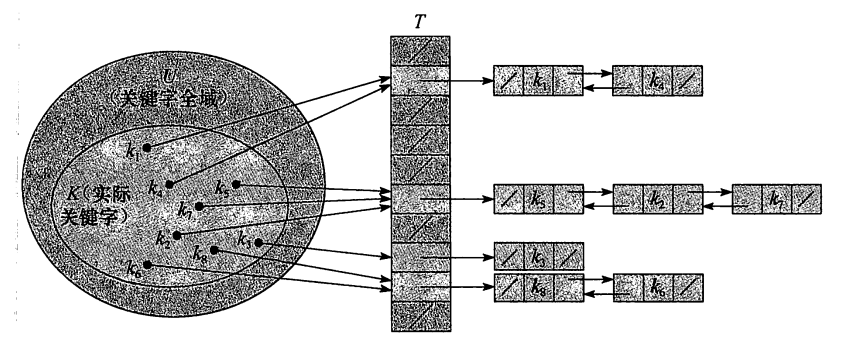
链接法

将散列表做成一个链表的集合，在通过散列函数$h(x)$求得值后，在其所对应的链表中进行比对寻找。

时间复杂度为$O(a+1)(a为链表长度)$

因为散列函数的时间复杂度是$O(1)$

散列函数

散列函数就是一个很普通的数学公式，将一个数映射到另一个数，如通过$\bmod$，等等方式。

但是，由于散列函数存在冲突，所以当一个散列函数被确定的时候，可以通过制造一些特定的数据，来使得散列函数的时间复杂度最劣。

我们希望能够有一个散列函数对于任何数据都有着良好的时间复杂度，若专业来说就是如下。

一个最简单的全域散列函数就是$h_{ab}(k)=((ak+b)\bmod p)\bmod m a和b\le p-1且属于Z,p为全域,m为映射后的域$，通过一些数论的知识可以证明。

开放寻址法

每一个散列表的槽只能放一个元素，因此散列表的大小需要大于关键字的数量。插入的方法就是按照位置的一个排列的顺序去找空位，若有空位，则插入。

此处，为了保证这个排列是均匀散列，即探查序列的排列需要是等可能的所有排列中的任何一种，需要去设计探查的方法。

所有的探查方式的探查顺序都通过一个函数来实现， $i^{'}=h(k,i)$。

线性探查

$h(k,i)=(h^{'}(k)+i)\bmod m$

二次探查

$h(k,i)=(h^{'}(k)+c_1i+c_2i^2)\bmod m$

双重散列

$h(k,i)=(h_1(k)+ih_2(k))\bmod m$

优劣

双重散列>二次探查>线性探查

实际应用双重散列

1. 取m为2的幂，并使h2总产生奇数
2. 取m为素数，并使h2总是产生比m小的正整数

时间复杂度分析

插入：$\frac{1}{1-a}$

查找：$\frac{1}{a}\mathrm{ln}\frac{1}{1-a}$

a为装载因数，即$\frac{插入的个数}{散列表的大小}$

完全散列

将链表法的链表改为一个散列表，使其大小$m_j=n_j^2$，即放入该槽元素个数的平方。

可以证明，冲突的概率小于0.5**(定理1)**，因此可以多次随机散列函数，即可找到一个不冲突的散列函数。

当n比较大的时候，可以进行第三次散列。

💡 我不确定是不是这个意思，下面是原话

还可以证明，总的空间复杂度为$O(n)$(定理2)。

且，总存储空间大于4n的概率小于0.5。

因此得出的结论如上。