数学建模

流程

1. 问题假设（要全面）
2. 模型建立
3. 模型求解
4. 模型评价

问题类型

1. 预测类

   用以往的数据来预测将来的数据

2. 评价类

   通过建立评价指标体系来评价一个东西

3. 机理分析

4. 优化类

   最优化理论，目标函数，变量，约束

Matlab

[]	矩阵，其中的数值可以是矩阵
；	换行
，或者直接空格	分列
while condition
end	循环
if condition
end	条件
diag(行向量)	对角阵
zeros(x,y)	x行y列的0矩阵
ones(x,y)	同上
rand(x,y)	同上，不过数据是随机的
eye(x)	大小为x的单位矩阵
clear	清屏
plot(x,y,点的图案样式)	画点
%	注释
，	，
function 返回值(如果是多个，则用一个矩阵返回)=函数名(参数)	函数
&&
Inf	无穷大
pi,sin,cos
矩阵(m,n)	矩阵中的第m行n列的那个元素
矩阵(m:n,m1:n1)	矩阵中m行到n行其m1到n1列的元素，:前后可省略
find(矩阵判断条件)	对矩阵中的每一个元素进行这个判断条件，返回满足条件的元素的位置
isempty
nargin	函数的输入参数数量
disp(变量/常量)	输出
size(矩阵)	返回一个1*2的矩阵，代表其行与列的阶数
eig(矩阵)	返回一个1*2的矩阵，第一个为特征向量的矩阵，第二个为特征值的矩阵，是对角阵，顺序一致
clc,clear	清空
repeat(矩阵,n,m)	将矩阵复制n行m列，返回一个矩阵
min/max(矩阵)	找矩阵中最小/大的
norm(矩阵)	平方和的根号，不知道是不是限制一行或一列
sort(矩阵,’descend’/’ascend’)	返回一个1*2的矩阵，第一个为排好序的矩阵，第二个是排好序的原来的序号
cumsum(矩阵)	对矩阵的行一次累加
mean(矩阵，参数）	求平均，当参数为2时为每行求平均
figure	创建一个新的视图

数学概念

剩余变量：通过引入一个变量来将不等式约束转为等式约束，如$x_1+x_2\le10，则x_1+x_2+x_3=10，x3\ge0$。

线性规划

目标函数是变量的线性表达式，变量有线性约束，使目标函数最优化。

线性规划标准式：

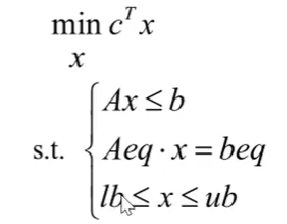
下面三个全是约束条件。A，Aeq都是矩阵，而剩下的全是列向量，当某一部分不存在约束的时候直接取空向量或者空矩阵即可。

求解命令：

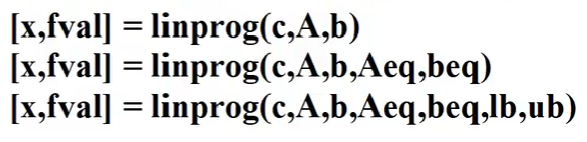
若要求最大值或者大于等于时通过取负来解决。

转换

1. 有时候式子并不是直接的线性表达式，此时可以通过转化来操作。

   如绝对值相加可以设$x_i=u_i-v_i,\ |x_i|=u_i+v_i$。

2. 将多目标规划转化为线性规划，如将目标转换为约束（即枚举约束情况来看总体的变化来找总体的最优）或将多目标转换为单目标

linprog

实际上linprog还会返回第三个值，若为负，则表示不存在可行解。

linprog还可以传入一个参数，option来控制其迭代设置（linprog求解过程是一个迭代过程）。

option是一个optimset返回对象。

optimset(oldoption(可省略),’param1’,value1,’param2’,……)。将oldoption中对应的param设置值。

Display	off不显示输出。iter每次迭代显示结果。final值显示最终结果。notify只在函数不收敛的时候显示结果
MaxFunEvals	函数中求值运算的最高次数。(一次迭代可能多次求值？)
MaxIter	最大迭代次数
TolFun	函数迭代的终止误差
TolX	结束迭代的X值？

整数规划（可以直接使用intlinprog,第二个参数表示第几个x为整数）

intlinprog好像在2014版的matlab就推出了。

当线性规划中的变量中部分（混合）或者全部（纯）被限制为整数时。

整数规划对应的线性规划被称为松弛规划。

1. 暴力所有可行整数解（当可行解较少时）

2. 分支定界法（已实现）

   对于求出来的松弛规划的解，选择第一个非整数变量，通过增加其向上取整或向下取整的约束条件来缩小可行域，对于新算出来的解，同样选择第一个非整数变量（递归），直到所有解都是整数，以求出可行整数解。如对于求出来$x1=2.3,则可添加x_1\le2或者x_1\ge3来$约束。如果求不出整数解，则换方法。

   实际上就是找边界周围的整数解进行暴力，并不断依此来缩小边界。

3. 割平面法（好愚蠢的算法，感觉劣与分支定界法）

   只适用于存在不等式约束的时候？

   基本思想：将没有整数可行解的平面切掉

   原理：通过将不等式约束引入松弛变量化为等式约束，后通过将小数部分与整数部分分离，得出对于某一个$x_i$的切割约束条件。

   最后一步的右式由于$f_i<1\&\&\sum[f_{ik}]x_k>0,则右式\le0$。得出$x_i$的约束。

   

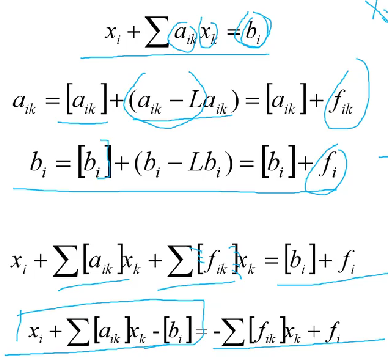
   1. 匈牙利算法（用于0-1整数规划）

      除去普通的人员分配问题（通过等式约束）（对于非标准的指派问题通过增加虚拟人或物及设定代价为无穷大来处理），还可以处理约束冲突问题（即当有两个约束是二选一的时候），此时可以引入一个新的0-1变量，表示使用哪一个约束条件，通过在约束右侧增加一个yM和(1-y)M，M是一个大数，来使得其在一个约束条件不起作用的时候另一个约束条件起作用。

      $$A_1x\le b_1+(1-y)M\\A_2x\le b_2+yM$$

      这一点可以推广，对于p个约束条件中选取q个约束条件。

      $$A_ix\le b_i+My_i\\\sum y_i=p-q$$

      基本原理：应该是贪心

      实现代码：复杂的一逼，傻逼匈牙利人（c++写完第二步就已经快100行了艹）

      实际实现代码：普通的进行约束进行普通的线性规划就可以了（好像并没有限定必须是整数，但是可能这样求出来的必然是整数吧？当然也可以直接使用intlinprog更保险）

非线性规划

目标函数与约束条件中包含非线性函数。

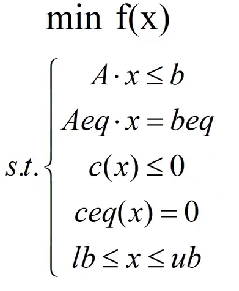
$c(x)与ceq(x)$是非线性函数的不等式约束与等式约束。$f(x)$可能是线性的也可能是非线性的。

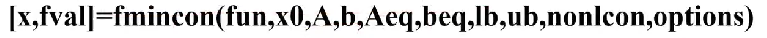
fun是一个字符串，为一个function的名字。这个function输入参数是x列向量，返回值是fv。

nonlcon也是一样是一个字符串，为一个function的名字。这个function返回的是[g,h]，g是不等式约束，h是等式约束。g与h都是矩阵，也就是说，当有多个不等式或等式约束的时候，g与h可能都是多行的。

例：

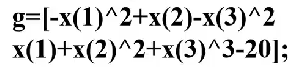
x0是x的初值，这个rand就好了。

二次规划

目标函数为二次，但约束都是线性，H是一个实对称矩阵。在输入H的时候要注意前面的0.5系数。

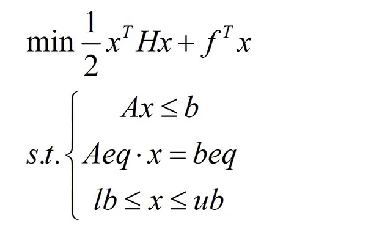
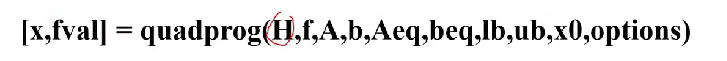
多目标规划

将多目标转化为单目标

1. 目标转约束
2. 加权相加
3. 分层序列法（求出一个的最优质值，然后在这个最优质值的限定下求下一个，往复）
4. 让最糟糕的目标最不糟糕

goal就是在分别不管其他目标下的最优值，一个列向量。weight各个目标的权重。fun是列向量，表示目标函数。

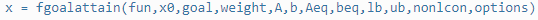
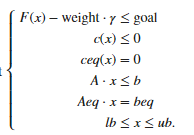
层次分析法 (主观赋权)

一个选择有多个因素决定，但因素之间的重要程度难以比较。

层次分析法通过两两比较的方式来确定因素之间的相对重要性。

主要用于选择与评判标准的制定上。

具体过程：

1. 建立层次分析模型

   分为三层：目标层（要解决的问题），准则层（决定方案好坏的要素），方案层（所有可能的解决方案）

2. 构造判断矩阵

   即因素两两之间的重要程度的相对比较，1-9表示从一样重要，到一个因素比另一个因素极端重要。而其在矩阵对称位置的元素与本元素相乘为1，也就是说所有元素的范围都在$\frac{1}{9}$-9。

   若是矩阵表示的这些相对关系连乘的结果与矩阵中的结果一致，则该矩阵为一致阵（有着如行列式等于1神奇的性质）。层次分析法允许不一致阵。

3. 层次单排序及一致性检验

   假设判断矩阵为n阶方阵，λ为判断矩阵的最大特征值，我们以λ-n的大小来衡量判断矩阵的不一致程度。

   一致性指标：$CI=\frac{\lambda-n}{n-1}$。越小越一致。

   RI为随机一致性指标（可查）。

   当$CR=\frac{CI}{RI}<0.1$时，则通过一致性检验。

   特征值所对应特征向量的每个数字代表该因素对总体的重要程度。

   但实际计算非常麻烦，可以通过一些方法来简化计算，得出一个不是那么精确的值。

   将判断矩阵的每一列列向量归一化（使这一列加起来为1），将归一化后的矩阵行元素相加，得到和列向量，将此作为特征向量，进行计算得λ。

4. 层次总排序及一致性检验

   将方案层对于每一个准则层的因素求一次单循环，假设第j个因素得出的$CI_j$，这每一个单循环的出来的CI都需要检验，而第三步得出的特征向量为$a_i$，也就是第i个因素的重要程度，得出总排序的CR。

   $$CR=\frac{\sum a_iCI_i}{\sum a_iRI_i}$$

   这一总排序的一致性比率也需要通过检验。

而最终第k个方案的最终权重为$\sum a_iw_{ik}$，$w_{ik}$代表对于第i个因素第k个方案的权重，也就是对第i个因素求出的特征向量的第k个值。

实现上，很简单。也可以直接使用它给的AHP”软件”。

如果提供的数据不需要两两比较就存在一个整体的顺序，那么直接构建一个一致阵就可以了。

优点

1. 系统性。把所研究的问题看成一个系统，按照分解、比较判断、综合分析的思维方式进行决策分析，也是实际中继机理分析方法、统计分析方法之后发展起来的又一个重要的系统分析工具。
2. 实用性。把定性与定量方法结合起来，能处理许多传统的优化方法无法处理的实际问题，应用范围广，而且将决策者和决策分析者联系起来，体现了决策者的主观意见，决策者可以直接应用它进行决策分析，增加了决策的有效性和实用性。
3. 简洁性。具有中等文化程度的人都可以学习掌握层次分析法的基本原理和步骤，计算也比较简便，所得结果简单明确，容易被决策者了解和掌握。

局限性

局限性是粗略、主观。首先是它的比较、判断及结果都是粗糙的，不适于精度要求很高的问题。

其次是从建立层次结构图到给出两两比较矩阵，人的主观因素作用很大，使决策结果较大程度地依赖于决策人的主观意志，可能难以为众人所接受。

TOPSIS (理想解法) (客观赋权)

将数据标准化并得出最优点（每一个因素都取最优）与最劣点，并计算数据点与其的距离来判断优劣。

过程：

1. 数据标准化
2. 将数据根据因素权重进行加权，也就是乘上因素权重
3. 确定两点
4. 计算距离（$s_优和s_劣$），以欧式距离作为距离
5. 计算各个数据的综合评价指数，$f_i=\frac{s_优}{s_劣+s_优}$

数据标准化总共要处理三个问题：

1. 将效益型（越大越好），成本型（越小越好）与区间型统一。
2. 去量纲
3. 归一化（将所有数据变换到[0,1]上）

标准化的方法总共有5种：

1. 线性 (不常用) ：$a^{'}=\frac{a}{a_{max}}$
2. 标准0-1变换：$a^{'}=\frac{a-a_{min}}{a_{max}-a_{min}}$
3. 区间型变换：分段函数，区间前与区间后各以成本型与效益型来处理，最终会分为五段，形状像梯形。
4. 向量规范化 (topsis中常用) ：

$$a^{'}=\frac{a}{\sqrt{\sum a_i^2}}$$

1. 标准化处理 (常用) ：

$$a^{'}=\frac{a-\overline{a}}{s_j}\ \ \ \ s_j=\sqrt{\frac{\sum (a_i-\overline{a})^2}{m-1}}$$

可以直接使用zscore(矩阵)。

聚类分析

将相似的分为一类，相似指的是关键值的差值很小。

• R型分类

  对指标进行分类，通过了解指标的相似程度，来一定程度上省略一些指标

• Q型分类

  对样本进行分类，比传统的分类方法更细致，全面，合理

1. 样本之间的距离度量

   欧式距离，$\sqrt{\sum(x_{ik}-x_{jk})^2}$，pdist(x)，x是矩阵。

   绝对距离，$\sum|x_{ik}-x_{jk}|$,pdist(x,’cityblock’)

   明式距离，$^m\sqrt{\sum(x_{ik}-x_{jk})^m}$，pdist(x,’minkowski’,m)。

   切式距离，$max|x_{ik}-x_{jk}|$

   方差加权距离，$\sqrt{\sum\frac{(x_{ik}-x_{jk})^2}{s_k^2}}$

   马氏距离，pdist(x,’mahal’)

pdist返回的是一个行向量，要通过squareform(行向量)来获得实对称矩阵

并可以通过tril(矩阵)来获得上三角矩阵

1. 变量之间的相似度量——相似系数

   用余弦或者相关系数。

   余弦：也就是点乘除上两个向量的长度。

   先用normc(矩阵)将矩阵单位向量话，最后a’*a即可得到余弦。

   相关系数：向量变为从向量的平均向量指向这个向量，也就是所有的x_i减去x均。

   corrcoef(矩阵)可直接求得相关系数。

2. 类间距离，代表两个聚类之间的距离

   最长距离，最短距离，平均距离，重心距离

3. 聚类方法

   • 谱系聚类法

   计算得到距离矩阵。

   设定类间距离大小。

   所有的点一开始都是一个类。若两个类的类间距离小于设定的，那么就合并。

   通过linkage(距离矩阵,’类间距离定义’)

   最短	空
   最长	complete
   中间	centroid
   重心	average
   离差平方和	ward

   其linkage将会做到直到只剩一个类。可以通过dendrogram(矩阵)来将linkage的过程可视化，linkage返回值作为输入。并可以通过cluster(矩阵，聚类几次）来输出聚类步骤。

   • k-means

   一开始定下聚类的个数。并随机这么多个数的随机聚类中心。

   将每一个点归类，并以这些归类的点计算出新的聚类中心。重复操作。

   可以直接使用kmeans(矩阵,个数)。

灰色关联分析（评价）

认为所有指标是等权重的。

对于一个选择，先量纲化处理所有方案的数据。

接着得出参考数列（一般取最优即可）

计算相差矩阵，也就是每一个元素改为其与最优值的差值的绝对值。

接着得出相差矩阵的元素最小值Xmin和元素最大值Xmax。

最终每一个选项在每一个指标的得分计算为$\frac{Xmin+p*Xmax}{Xnow+p*Xmax}$，p为分辨系数，一般取0.5。Xnow就是这个相差矩阵的这位元素的值。

最终将所有指标得分平均即为这个选项的得分。

如相差矩阵为

1	1
2	0

则Xmin为0，Xmax为2。

则为$\frac{0+2*0.5}{1+2*0.5}$。1为该位置元素的值。

灰色预测模型（预测）

基本思想：现实数据存在随机性，通过累加、累减、加权累加等方式来消除随机性找到规律进行预测

步骤：

1. 进行检验与处理

   要使用灰色预测模型，必须首先经过级比检验

   $$设原数据为x^{(0)}(i),i\le n,需保证\lambda(k)=\frac{x^{(0)}(k-1)}{x^{(0)}(k)}\in(e^{\frac{-2}{n+1}},e^{\frac{2}{n+1}})对k\ge 2恒$$

   若不符合，可以通过使$x^{(0)}(i)'=x^{(0)}(i)+c$平移操作来使符合，但不要忘记预测时要逆操作。

2. 建立GM(1,1)模型

   $$灰微分方程为\ :\ x^{(0)}(k)+az^{(1)}(k)=b$$

   $$其中x^{(1)}邻值生成数列z^{(1)}(k)=ax^{(1)}(k)+(1-a)x^{(1)}(k-1),a一般取0.5$$

   $$其中一次累加生成数列x^{(1)}(k)=\sum^k_{i=1}x^{(0)}(i)$$

   $$设u=\begin{bmatrix}a\\b\end{bmatrix}=(B^TB)^{-1}B^TY,其中B矩阵为\begin{bmatrix}-z^{(1)}(i)&1\end{bmatrix}\\Y矩阵为\begin{bmatrix}x^{(0)}(i)\end{bmatrix},i\ge2\\$$

   $$解得后x^{(1)}(k+1)=(x^{(0)}(1)-\frac{b}{a})e^{-ak}+\frac{b}{a}\\预测值x^{(0)}(k+1)=x^{(1)}(k+1)-x^{(1)}(k)$$

   1. 进行检验正确性

      a. 残差检验

      $$\varepsilon(k)=\frac{x^{(0)}(k)-x_预^{(0)}(k)}{x^{(0)}(k)}$$

      若所有$|\varepsilon(k)|<0.1$，这达到较高的要求。若所有$|\varepsilon(k)|<0.2$，这达到一般要求。

      b. 级比偏差值检验

      $$\rho(k)=1-\frac{1-0.5a}{1+0.5a}\lambda(k),此处\lambda(k)为前面第一步中的,a一般取0.5$$

      若所有$|\rho(k)|<0.1$，这达到较高的要求。若所有$|\rho(k)|<0.2$，这达到一般要求。

      二者中达成一个即可。

数据预处理

即便没有需要预处理的，也需要进行说明。

总共四种。

1. 数据清洗

   1. 异常值

      一般直接视为缺失值或者用前后的两个数据平均作为数据

      重点在于如何判断是否是异常值。

      1. 将正态分布中＞3σ的作为异常值

      2. 箱线图。假设Q1是第25%的数据的值，Q3为第75%的值，IQR=Q3-Q1，将>Q3+1.5IQR和<Q1-1.5IQR的视为异常值

         使用boxplot绘制箱线图，用法boxplot(矩阵)，会为每一列绘制一个

      3. 通过散点图肉眼观察

         如果不用肉眼的话，可以设定一个特定的距离。如果对于某个点来说有超过n个点与它的距离大于这个设定的距离，那么这个点就是散点。距离和n都是要人为主观设定的。

   2. 缺失值

      1. 直接删除这一组数据
      2. 不处理，作为一种特别的数据
      3. 数据插补

      其中，插补的方法有多种。

      1. 直接将其取为均值，中位数，或众数

      2. 直接将其取为固定值

      3. 回归邻插补，找到“距离”最小的另一个数据点，直接用它的这一个数据

      4. 回归方法，通过其他的正常数据拟合模型来预测

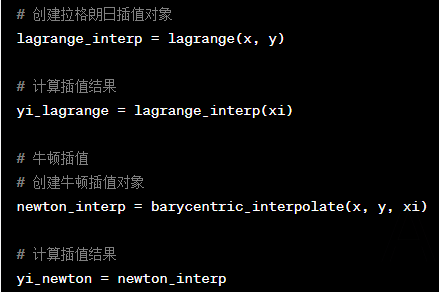
      5. 插值法，使用合适的插值函数，依靠拉格朗日插值法或牛顿插值法

         实现方法：

         ployinterp_column(有空缺的矩阵，’lagrange’或’newton’)返回一个插值完的矩阵

         这是由它写的函数实现的，matlab本身并没有直接的方法

         python中倒是在scipy库中有可以直接使用的函数。

         可能不一定是下面这样用的？(chat写的）

         

2. 数据集成

   将多个数据库的数据集成为一个统一的数据库

3. 数据消减

   在很多情况下，有一些数据是完全与结果无关的或者与另一个因素是有非常强的关联的时候可以将这一部分数据给去除，减少数据量，提高效率，而不降低正确性

   1. 研究特征之间的关系
   2. 暴力枚举选取因素，选取预测最好的

   两个因素的相关性可以用斜方差来表示

   $$cov(x,y)=\frac{\sum^n_{i=1}(x_i-\overline{x})(y_i-\overline{y})}{n-1}$$

   可以通过这个来生成一个斜方差矩阵，再通过主成分分析法来降维。

   可通过corrcoef(矩阵)，返回斜方差矩阵

   并通过pcacov(斜方差矩阵）进行主成分分析法，返回[矩阵,~,矩阵]，第一个矩阵代表主成分分析法新造出的几个主成分的原因素系数，最后一个矩阵代表每一个成分的贡献度，只需要从前往后进行累加，当累计贡献率＞85%时，剩下的就都可以被抛弃了。

   当我们得出几个新的因素由原因素线性表示的时候，我们不仅要写出表达式，也需要对此进行实际意义上的阐释。

4. 数据变换

   1. 归一化

      保证量纲一致

   2. 函数变换

      当存在偏态分布而非正态分布时，可以通过指数函数与对数函数分别将左偏与右偏数据调整为正态分布，这样能够当我们用某几个指标衡量的时候得出的结果会相同，或者可以使用某些对数据要求很严格的检验

插值

1. 拉格朗日插值法

   对于n个$(x_i,y_i)$的点，我可以生成n个$f_i(x)$使得它在$x_i$的值为1，而其他的x点上都为0。

   此时$f(x)=\sum_{i=1}^ny_if_i(x)$必然会经过所有点。

   而$f_i(x)=\prod_{j=1}^n\frac{x-x_j}{x_i-x_j}$。

   用的较少好像

2. Runge现象

   当多项式的次数变高，插值函数的边缘处会出现非常大的震荡，因此一般不建议次数超过7。

   这可以通过分段插值来解决，也就是很多个点几个连续的分为一段，对他们分别进行低次插值。

   因为我们想进行的仅仅是插值而非拟合，所以不用管分段对于整体的问题。

3. 一维插值

   interp1(x,y,x_i,’method’)，x_i可以是一个矩阵，返回的y_i大小与x_i相同

   method有

   nearest	最邻近插值
   linear	线性插值
   spline	三次样条插值	一维用，看起来是最好的
   cubic	立方插值	二维用

4. 二维插值

   interp2(x,y,z,x_i,y_i,’method’)

   method与一维的一致，只不过linear和cubic的中文名都加上一个双

5. 散点插值

   上述的都是已有的数据点都是大量的，但常常有那种只有零星几个点的，此时就应该用散点插值

   griddata(x,y,z,x_i,y_i,’method’)，其他与二维插值差不多

回归

1. 一元线性回归

   1. 求出方程的系数

      设预测值为$y'$，则将$\sum(y-y')^2$作为评估误差大小，将$y=\beta_0+\beta_1x$代入，会得到一个关于$\beta_0$和$\beta_1$的二次函数，通过导数求其最小值，得

      $$\begin{cases}\beta_0=\overline{y}-\beta_1\overline{x}\\ \beta_1=\frac{\sum (x_i-\overline{x})(y_i-\overline{y})}{\sum (x_i-\overline{x})^2}\end{cases}$$

   2. 对求出的系数进行假设检验，$1-\alpha$为置信度，$\alpha$一般取0.05。

      1. F检验法

         $$F=\frac{U(n-2)}{Q_e},Q_e=\sum (y_i-y_i')^2,U=\sum(y_i'-\overline{y})^2$$

         此处的$\overline{y}$应该是原y的平均值。

         当$F>F_{1-\alpha}(1,n-2)$时，则方程通过检验。后面的值可依靠查表得。

      2. t检验法

         $$T=\frac{\sqrt{L_{xx}}\beta_1}{\sigma_e},L_{xx}=\sum(x_i-\overline{x})^2,\sigma_e^2=\frac{Q_e}{n-2}$$

         其中$\overline{x}$也应该是原x的平均值。

         当$|T|>t_{1-\frac{\alpha}{2}}(n-2)$时，则方程通过检验。后面的值可依靠查表得。

      3. r检测法 ?为什么公式里一个预测值都没出现

         $$r=\frac{\sum(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum(x_i-\overline{x})^2\sum(y_i-\overline{y})^2}}$$

         当$|r|>r_{1-\alpha}$时，则方程通过检验。后面的值可依靠查表得。

      算出来的$\beta_0$和$\beta_1$也是有一个不确定度的。

      $$\beta_0=\beta_0\pm t_{1-\frac{\alpha}{2}}(n-2)\sigma_e\sqrt{\frac{1}{n}+\frac{\overline{x}^2}{L_{xx}}}$$

   3. 对x0做预测或对y做区间估计

      1. 预测

         预测得的$y'$也有一个不确定度。

         $$y'=y'\pm\delta(x_0),\delta(x_0)=\sigma_et_{1-\frac{\alpha}{2}}(n-2)\sqrt{1+\frac{1}{n}+\frac{(x_0-\overline{x})^2}{L_{xx}}}$$

      2. 区间估计

         当我们希望y有$1-\alpha$的概率落在$(y',y'')$上时。

         假设最终的区间为$(x',x'')$。

         其分别为$y-\delta(x)=y'和y+\delta(x)=y''$的解。

2. 可化为一元线性回归的非线性回归

   • 非线性回归的实现

     [beta,r,J]=nlinfit(x,y,’model’,beta0)

     或者nlinttool(x,y,’model’,beta0,alpha)

     r为残差。

     J为雅可比矩阵。

     model是一个定义的函数。

     beta0为系数初值，随意设即可。

     预测使用[y,$\delta$]=nlpredci(’model’,x,beta,r,J)

   通过$\begin{cases}v=v(y)\\u=u(x)\end{cases}$，使得u与v是线性相关的，找到u和v的关系后通过逆函数再还原为y和x即可。

   常用的非线性函数。

   $$y=a+\frac{b}{x},\frac{1}{y}=a+\frac{b}{x},y=ax^b,y=ae^{bx}\\y=ae^{b/x},y=a+blnx,S型\ y=\frac{1}{a+be^{-x}}$$

3. 多元线性回归

   1. 计算

      $$Y=X\beta,Y=\begin{bmatrix}y_i\end{bmatrix},X=\begin{bmatrix}1\ x_{i1}\ x_{i2}\ \dots\ x_{ik}\end{bmatrix},\beta=\begin{bmatrix}\beta_{0,1,\dots,k}\end{bmatrix}$$

      $$通过最小二乘解得,\beta=(X^TX)^{-1}(X^{-1}Y)$$

      当碰到多项式回归时，只需要使$x_i=x^i$即可，化为多元线性回归。

      • 对于多项式回归的实现

        [p,S]=polyfit(x,y,m),m为最高次次数。

        $p=(a_1,a_2,\dots,a_{m+1}),a_i为x^{m-i+1}的系数。$

        通过y=polyval(p,x)来进行预测。

        通过[y,$\delta$]=polyconf(p,x,S,alpha)。

        得到其在x处的预测值及估计区间。

      • 多元二项式回归

        或者直接将其转化为多元线性

        rstool(x,y,’model’,alpha)

        窗口左边会显示y与置信区间

        最后将结果export出来，会获得beta和rmse，只要rmse<10就不错了。

        

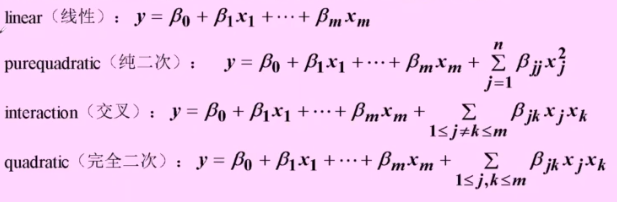
   2. 检验

      F检验

      $$F=\frac{U(n-k-1)}{Q_ek}>F_{1-\alpha}(k,n-k-1),其他与一元一致$$

   3. 实现

      [b,bint,r,rint,stats]=regress(Y,X,(alpha)),对于一元和多元是一样的。

      bint为b的区间估计。

      r为残差，也就是每一个y’与y的差值,rint为它的置信空间。

      stats=[$r^2$,F,F对应的概率p]。

      $r^2$越接近1越好，F越大越好。

      可以通过rcoplot(r,rint)来画出残差与置信区间。

4. 逐步回归

   一些变量可能实际与y无关，此时通过暴力枚举的方式，选选去去变量，来找到那个最好的方案。

   • 实现

     stepwise(x,y,inmodel(一般空缺),alpha)
     会出来一个图形窗口，一般直接next step即可，matlab会自动进行逐步回归。

     如果希望手动操作的话，点击左边窗口内的条条即可去掉或选择变量。

     尽量使R.square接近1，且F增大。当变化不大时尽可能保留更多的变量。

拟合（预测）

小样本。

当需要预测提供数据范围之外的数据的时候，应使用拟合。插值对于数据范围之外的数据会因为runge0现象而波动较大。

拟合更重要的是求函数关系，而插值是更关注函数值。

而插值必是过所有已知点的，而拟合不一定。

线性一般使用最小二乘，而非线性一般使用牛顿。

1. 多项式拟合

   见回归.3

2. 非线性拟合

   见回归.2

3. 可视化拟合（拟合工具箱）

   通过命令cftool启动。

   其中输入x data与y data，可以直接导入存储在工作区中的变量

   通过右上角的更改可以更改想要拟合的函数类型，函数类型如下。

   或者直接在下方直接输入想要拟合的函数

   

   左侧的result就是拟合的结果。使SSE体验RMSE趋向0，r-square趋向1。

综合评价

评价类一般有几种，分类，排序与打分。

多个指标进行评价。

最终的权重函数一般有三种。

1. 线性加权（指标间没有较强关联性）

$$y=\sum w_ix_i$$

1. 非线性加权（指标间有较强关联性）

$$y=\prod x_j^{w_j}$$

1. topsis

模糊综合评价

对于一个事物，有多个指标，而对于一个指标，评价是多种的，且是模糊的，没有明确分界线的，如{好，中，差}。但是我们知道评价的比例。’

实际上，这里只是将评价的比例作为隶属度而已。隶属度才是真正通用的模糊综合的指标。而隶属度就表示对于这个指标来说对于某一个模糊评价的隶属度。

而通过将指标的权重（通过层次分析法(主观)或者变异系数法(客观)求得）（列向量）与评价矩阵（每一行是一个指标的隶属度）模糊相乘，得到的新的矩阵就是对于这一个事物整体的评价比例，对其进行归一化即可。

模糊相乘：原理与矩阵相乘一致，但是相加变为取最大值，相乘变为取最小值。

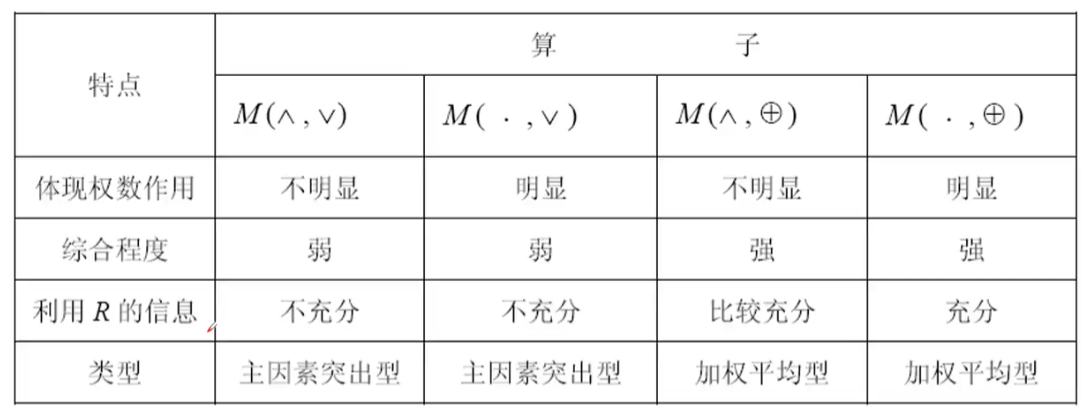
实际上模糊相乘有很多种，每一种被称为一种算子，上面的这种就是一种算子，各有各不同的优点。

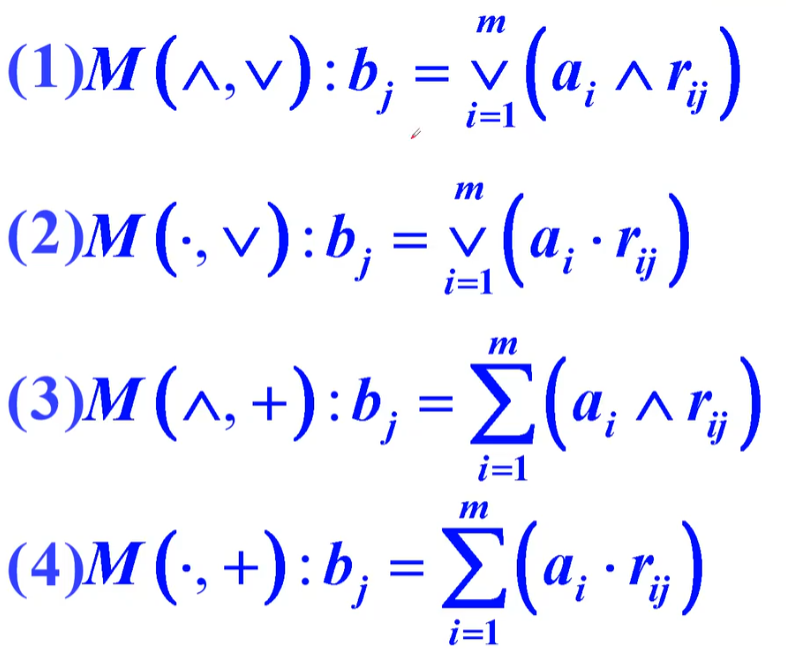
若一个指标是由多个二级指标决定的，那么，将这个指标当做事物，进行一次模糊综合评价即可。

除去算子有很多种，隶属度的得出也有很多方法。下述的两种方法（与灰色关联分析相似）算子一般都是用第4种。

1. 相对偏差评价法

   $$u_i=\begin{cases}max(x_i)\ 效益型\\min(x_i)\ 成本型\end{cases}\\r_{ij}=\frac{|x_{ij}-u_i|}{max(x_i)-min(x_i)}(一列列进行处理)$$

   越小越小

2. 相对优属度评价法

   $$r_{ij}=\begin{cases}x_{ij}/max(x_i)\ 效益型\\min(x_i)/x_{ij}\ 成本型\\min|x_{ij}-X_j|/|x_{ij}-X_j|\ 固定性\end{cases}\\X_j是第j个指标的适度值。$$

   越大越好

这两种与灰色关联分析法可以综合使用（得出的结果可能不同）

主成分分析

作用：数据的降维；数据的解释

主成分得出的综合指标数量与原指标数量一致，但是我们只取其中的一部分。

因子分析法得出的综合指标数量是被指定的。

主成分最终得出的指标的系数就是斜方差矩阵的特征向量。特征值除以特征值的总和就是贡献度。而这是由于当取特征向量的时候方差会最大，而这是我们所希望的。

一般选取主成分时有两种方式。

1. 累计贡献大于85%
2. 特征根>1

使用主成分分析必须保证其成分之间是有关联的。

为了保证有关联，需要进行检验，一般有两种检验方式。

1. kmo检验

   若>0.5，则非常适合。

   若>0.3，则可以，但不推荐。

   若<0.3，则不要。

2. bartlett’s检验

   若<0.05，则适合。

   若>0.05，则不适合。

上述的两个检验满足任意一个即可。

（好像spss中会自动检验，如果勾选的话？）

实现：

SPSS中：

使用因子分析法，描述中勾选初始解，与检验，提取中勾选选择主成分，斜方差，可以调整特征值，旋转不用管，得分要选择回归，且显示得分。

直接观察总方差解释，其中总计就表示特征根。

而后成分矩阵即为实际的系数。

都使用重新标注的（经过处理后的）。

但这里的系数是因子分析法的，而主成分分析法的因子就是因子分析法的因子/开根号的特征根。

变异系数法

由于如果数据的区别非常大，那么更容易来区分，给予它一个更大的权重。

变异系数法以标准差/均值作为$v_i$权重，最后对$v_i$归一化，作为最终的权重$w_i$。

但这必须保证重要性相当的情况。

四种基本变量

1. 定类变量（其中的种类是平等的，没有高低之分的）
2. 定序变量（其中的种类是有一个序的，但是不能定量）
3. 定距变量（其中的种类是有一个序的，但是能定量）
4. 定比变量（其中的种类是有一个序的，能定量，且存在0(没有)的概念，可以作乘除）

方法使用分类：

	定类	定序	定距
定类	卡方类检验	卡方类检验	Eta
定序		spearman	spearman
定距			pearson

1. pearson

   适用条件。测量的连续变量。正态分布数据。成对数据。线性关系。

   $$r=\frac{\sum(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum(x_i-\overline{x})^2\sum(y_i-\overline{y})^2}}\\t=\frac{r}{\sqrt{(1-r^2)/(n-2)}}$$

   r即为相关度，而t则需要t检验。当|t|>$t_\frac{a}{2}$时，则显著，若小于等于，则不显著。

   r的取值与相关程度。取正为正相关，取负则负相关。

   0.00-0.19	极低相关
   0.20-0.39	低度相关
   0.40-0.69	中度相关8
   0.70-0.89	高度相关
   0.90-1.00	极高相关

2. spearman

   $$r_s=1-\frac{6\sum (x_i-y_i)^2}{n(n^2-1)}\\t=r_s\sqrt{\frac{n-2}{1-r_s^2}}$$

   其中，xi与yi为其等级。n为样本量，当超过20时，要t检验。而检验基本与pearson一致。

上述两种的实现在spss中分析-相关-双变量中直接调用即可解决，可以在样式中更改输出内容。

1. 卡方检验

   实现：SPSS中分析-描述统计-交叉表，在统计中选择方法（卡方）。行是因变量，列是自变量。

   当皮尔逊卡方的渐进显著性<0.05时，则相关。

   如果数据是频数的，可以使用数据-个案加权来处理。

2. Eta

   实现：SPSS中分析-描述统计-交叉表，在统计中选择方法（相关性）。行是因变量，列是自变量。

   Phi>0.5，则相关。若Phi>皮尔逊R，则关系更有可能为非线性。

3. 偏相关

   一个因素可能与多个因素相关，若是我们只想研究二者之间的相关性，那么就需要控制其他变量。

   实现：spss中分析-相关-偏相关，变量中放入研究的几个变量，控制中放入需要控制的变量即可。（用的皮尔森？）

   检验也是t检验，直接看表中的显著性即可。

神经网络：大数据

元胞自动机：模拟

马尔科夫：概率转移，我的建议是直接暴力😀

国赛：颜色与物质浓度的辨识问题（回归+层次分析）

通过线性回归的置信区间，残差分析来确定数据的优劣，F,R^2,P,S^2，以及剔除点数量。

解释模型与代码，一一分析。

给出残差图，残差值，与四个指标，并给出原数据，在过程中如果有异常点，则剔除后再做一次，最后给出该回归模型。

通过分别尝试线性回归和二次回归来建立模型，比较优劣。

给出残差，显著性四个指标，并进行检验。

通过层次分析来确定非定量指标对于最终的影响因子。

层次分析图

国赛：校园供水系统智能管理（回归+神经网络）

对于找特征，需要涉及特征指标变量。在统计与计算过程中，可以列出，均值，方差，标准差，置信区间**？**(自由度=6/11)

并且要给出特诊指标变量的意义。

用图表表示给定数据。

回归过程中检验可以用SSE，SSR等更加专业的表示。

回归图中画出理论，实际与置信区间

神经网络写出模型建立，以及训练过程的图，与最终的结果。

国赛：葡萄酒质量的评价（回归，聚类，双因子可重复方差分析？）

回归前可以使用皮尔森或其他相关性分析去掉几个变量。

国赛：风电场运行状况分析及优化研究

在优化时考虑实际。

国赛：葡萄酒质量的评价

用正态分布检验来看统计结果

遗传算法解决非线性规划与多目标规划

信息不完全、不充分的预测系统——灰色预测

校赛：

1. 战争

   1. 兰彻斯特

   2. 仿真模拟

      System Dynamics and Multi-Agent Simulation Research on Ground CombatPersonnel Attrition.pdf

   3. 神经网络/回归预测

   4. 蒙特卡罗试验？

   5. 系统动力学

2. 共享单车

   1. （违规区域的划分与罚款金额的制定）

   2. 根据人的流量来进行投放（多商品流网络流(线性规划)，还要在最小成本的情况下，根据堵塞情况来决定流量大小，或者直接不要流量限制，直接最小成本）

      

      

   3. 对于各品牌的投放策略的改变（因为常常有有蓝车没绿车，有绿车没蓝车的情况）(博弈?)

   4. 预测使用需求（各种预测模型，小样本灰色）

   5. 马尔科夫来预测车辆损坏情况来确定维修策略