红黑树

性质

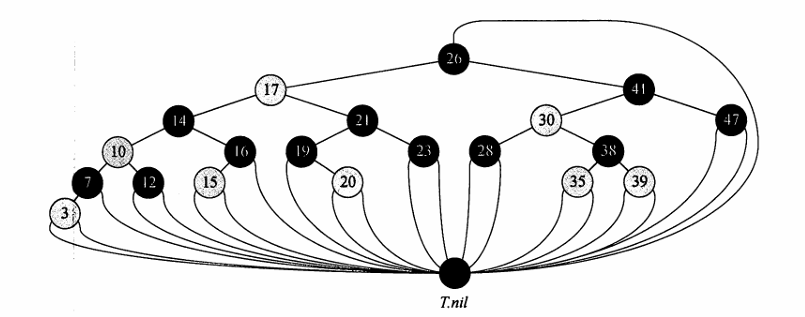
旋转

插入

插入的新节点或者需要调整的节点必然是红色的

当该节点的父亲是红色的时候，就需要调整。

情况一：叔节点是红色，将爷节点的黑色下放

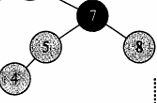
情况二：叔节点是黑色，当父节点是左节点时，本节点是左节点就右旋，右节点就左旋，有节点则相反，当与叔节点是异边节点时调整颜色

操作完成之后要么循环结束，要么矛盾节点上移产生新的矛盾

仍然没有搞懂为啥左节点的时候就不能左旋，虽然确实会不平衡，但为什么这样就会不平衡呢

删除

二叉搜索树的删除

情况一：要删除的节点有一个子节点不存在，将子节点替换掉本节点即可

情况二：两个子节点都存在，在右子树上找到第一个没有左节点的节点，将它替换掉本节点，其右子树直接上升

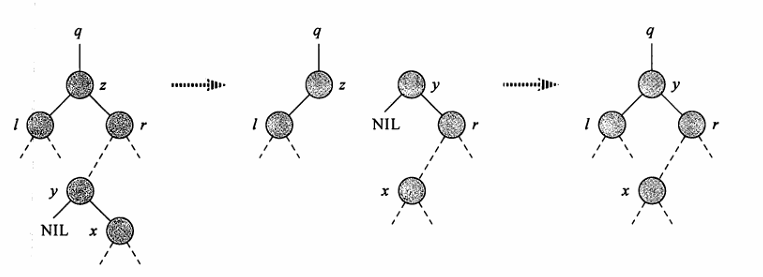
实现方法：tranplant函数，即用某节点替换某节点

红黑树的删除

无论是情况一还是情况二中，唯一会影响红黑树的正确性的就是y的移动，因此需要记录y的原始颜色。

情况一：y的原始颜色就是z的颜色。

情况二：y的原始颜色就是上图中y中的颜色。因为最后y的颜色会改为z的颜色，所有是y原本的颜色消失了。

而这一切的产生的违反性质的问题都将在x节点上反映出来，x为y的子节点。

不知道为什么有x是根节点的情况

当x为红色时，染黑即可。

当x不为红色为黑色时，将它变红。

为什么2,3,4的父节点是红的，如果节点是黑的是否有问题

情况一：如果兄节点是红的，将它转为黑的，变为情况2,3,4

情况二：如果兄节点的两个孩子都是黑的，可以将x一重黑与兄节点的黑色提到父节点，即可去除一重黑。

情况三：如果兄节点的左孩子是红的，右孩子是黑的，将其右孩子转为红色，转为情况4。

情况四：如果兄弟的右孩子是红的，直接解决。