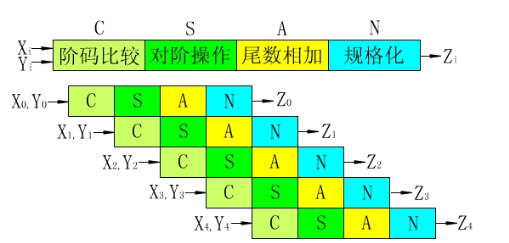
运算方法和运算器

小数：IEEE754

1位符号位

8位阶码（移码）补码的最高位取反（将指数变为正数）（+127）

23位尾数（原码）

符号位是尾数的符号位

最终的结果是1.尾数*10^阶码

当尾数和阶码全0时为0，因符号位有正0和负0

当尾数位0且阶码全为1为无穷大

当阶码为0而尾数不为0时，则为0.尾数*10^（-126）

当阶码为全1且尾数不为0时，则为Nan，一种非数值

浮点数有正负上下溢

奇偶校验码：加上校验码这一位是奇数个1还是偶数个1

补码取负：取反，末位➕1

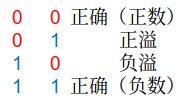
溢出判断：

1. 双符号位法，用两位表示符号位，在运算完后

   负则前两位为1，否则前两位为0

2. 单符号位，分别看符号位的进位和最高位的进位

乘法器：

1. 首先算出所有的部分积(第一个数字的某一位和另一个数字的某一位的积)
2. 一起输入阵列乘法器(实际执行的是加法)，进行相加(按列相加)。
3. 每一位的加法是，上面的和+当前位+前面一列这一行的进位

对于一个补码，要相乘。

1. 算前求补，变为原码（为n位)
2. 乘法
3. 算后求补，变为补码（为2n位)

原补互变的方式：

1. 符号位为0，不变
2. 符号位位1，从右往左找到第一个1，然后，从这一位左侧那一位到符号位之前都取反

对于电路来说，遇到第一个1后，或就永远是1了，然后当E也位1时，与出来就为1，也就是要取反了

除法器：

1. 定点原码除法，每次将除数右移，主要问题在于判断当前是商0还是1，要减一下看一下<=>0，然后还要加回来
2. 不恢复余数法，余数为正，商1，下一次右移做减法，为负，商0，下一次做加法

并行加法器：

普通的逐位加法器，被称为行波进位

并行：

第一种是，四位内并行，四位外行波。

$$G_i=Y_{4i+3}+Y_{4i+2}X_{4i+3}+Y_{4i+1}X_{4i+2}X_{4i+3}+Y_{4i}X_{4i+1}X_{4i+2}X_{4i+3}\\P_i=X_{4i}X_{4i+1}X_{4i+2}X_{4i+3}\\G_{ij}=G_{i(j-1)}X_{j}+Y_j\\P_{ij}=P_{i(j-1)}X_j$$

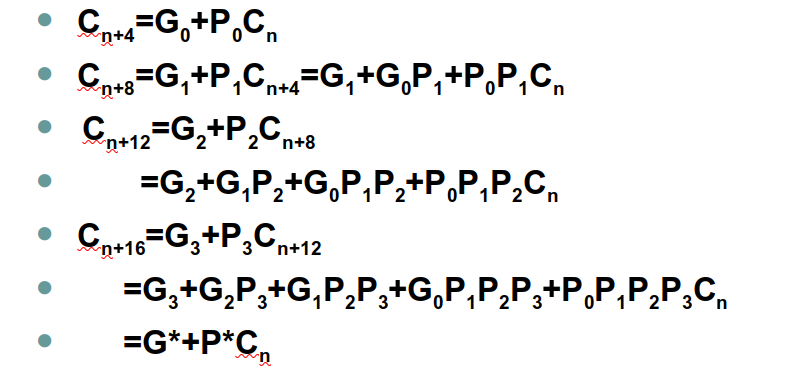
每一位的Ci可以先行计算，而在计算出所有G和P后也可以由C0计算出C4,8,12,16，而可以由AB算出所有的G和P，因此就可以先行算出所有的进位。

可以做到16位内并行，16位外行波。

总线：cpu内或者与外部设备的，有单向双向

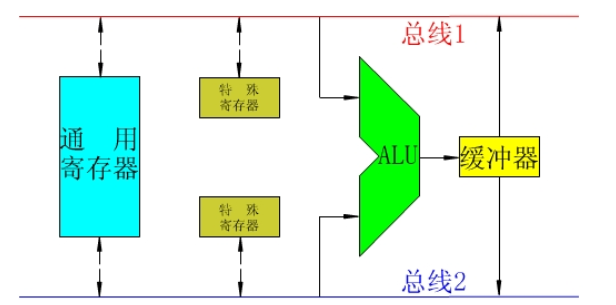
单总线：对于ALU前必须有暂存器，存下第一个，再存下第二个，然后计算，再返回，因为单总线所有的线只能存一个数据

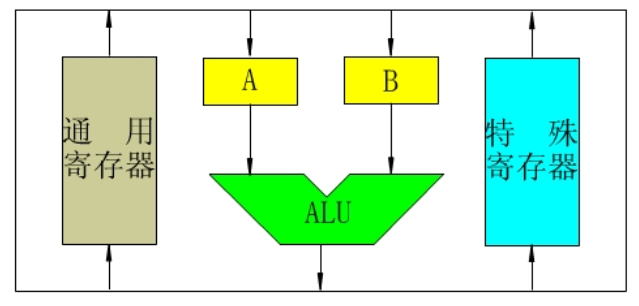
双总线：就不需要有暂存器了

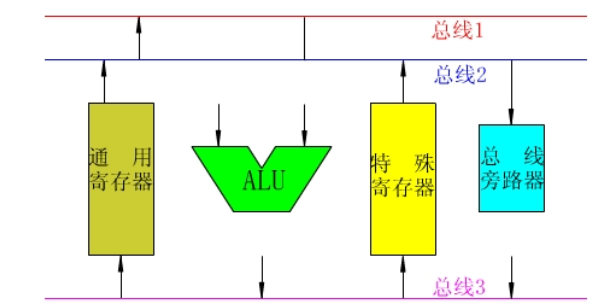
三总线：总线都是单向的了

浮点数加减：

1. 判断浮点数是否为0，因为0是人为定义的。

2. 统一指数，变为更大的指数，为了保证改变后仍然是1.M/0.M，求和结果大概率是1.M

3. 尾数求和/减

4. 结果规格化

5. 舍入处理

   1进0舍，如果是负数，则相反。

   朝+∞舍入：正数结尾不全为0就进，负数相反

   阶码上溢，一般将其认为是＋∞和－∞ 。
   阶码下溢，则数值为0。

乘除：

1. 检查
2. 阶码加减
3. 尾数乘除
4. 规格化+舍入

流水线操作：如对于浮点数计算，则将每个部分分为一个部分。